2 posts tagged with "epistemology"

A fractal is a way of seeing infinity

-- Benoît Mandelbrot

Nothing is built on stone; All is built on sand, but we must build as if the sand were stone.

-- Jorge Luis Borges

Can You Measure a Coastline?​

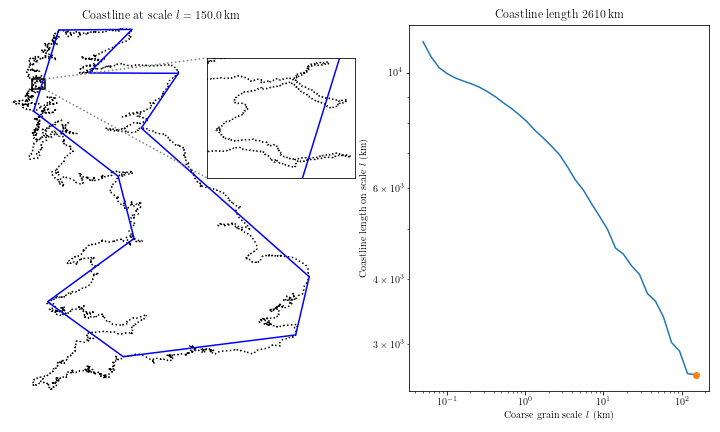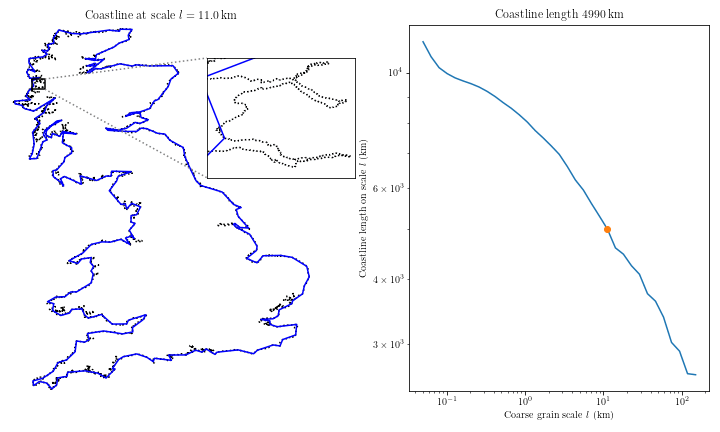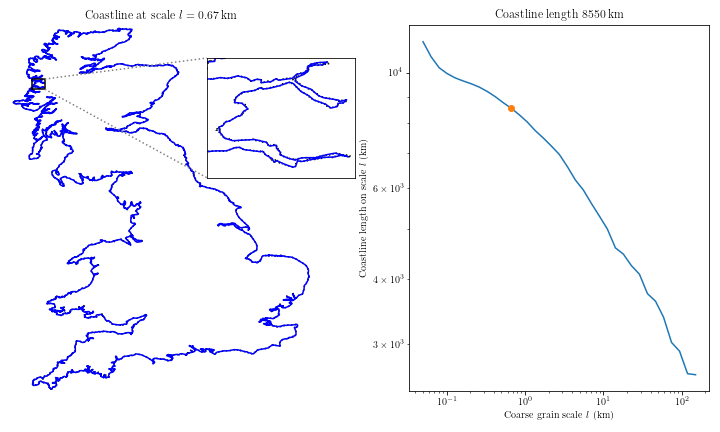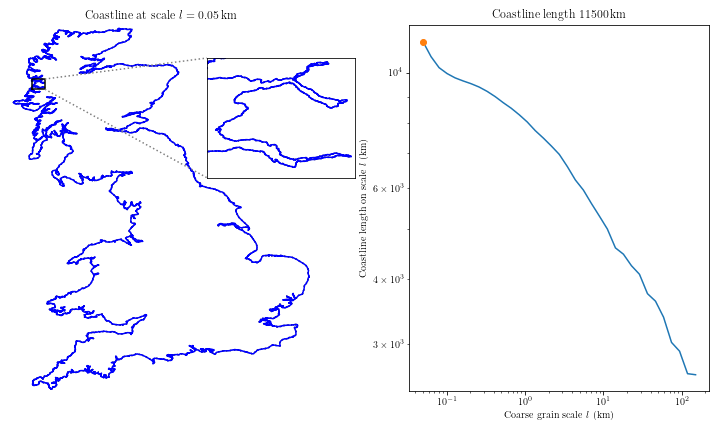
In 2006, the Congressional Research Service (CRS) of the United States estimated the coast of Maryland to be 31 miles long. Strangely, the National Oceanic and Atmospheric Administration (NOAA) estimated it to be 3,190 miles long. This staggering difference was not a clerical error. These values were the actual reported measurements from each study of the Maryland coastline. (For more see here)

Maryland's is not the first coast in history that cartographers have separately measured to wildly different lengths. The phenomenon is known as the "Coastline Paradox". When estimating the length of any fractal curve via straight lines, the actual length is indeterminate. Suppose I measured the coastline of Maryland with a yardstick, and you with a foot-long ruler. My answer will be far smaller than yours. Without getting into the math, the smaller your measurement-length, when measuring a fractal curve, the larger the length of that curve will be.

This measurement problem is known as the Richardson Effect and has been studied in detail by Benoît Mandelbrot. Mandelbrot famously described shapes with infinitely embedded and repeating complexity with very simple equations that describe what he called "fractals".

I will not go through the exact definition of a fractal here, but we can simply say for now that a fractal curve is defined as one whose perceived complexity changes with measurement scale.

In Mandelbrot's own words a fractal is, loosely:

a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole

When measuring any fractal shape, real or abstract, we face this coastline problem. Part of what it is to measure is to agree on something. It is on the basis of this embedded self-similarity of fractals that the "Coastline Paradox" is claimed to be a "Paradox". It is claimed that a coastline has no real determinate length, yet we can measure it to have some length.

Is there really a paradox here? I think in a trivial sense yes. I argue that real objects that exhibit fractal curves only have a determinate length insofar as we can agree on a measurement schema. Do we stop at the grain of sand? The Angstrom? The inch? The best answer will be determined by our goals, but that does not mean it will always be easily attained. It has been pointed out recently, on account of this goal-based agreement, that perhaps a coastline is not really fractal in the Mandelbrot sense.

A Strange Philosophical Question​

My purpose in this note is not mathematical or cartographic. I want to consider the "Coastline Paradox" as a model for our understanding of reality and pose some philosophical questions based on that comparison.

Mandelbrot considered his fractals to be related to a "theory of roughness". The relationship between a fractal edge and our concept of 'roughness' is easy to see in a physical object. Imagine zooming in on an aerial view of a coastline. The closer we get, the more the shape changes, and embedded patterns are revealed that are self-similar to the overall shape (in some sense, perhaps not exactly as in Koch Snowflake GIF at the start of this note).

The philosophical question I want to ask is this: what if our relationship to reality is analogous? What if the deeper we dig into some phenomena or some realms of understanding, the more embedded complexities we discover ad infinitum? This question decomposes into the questions of whether there is some infinite nature to the depth of inquiry and whether that infinite depth would exhibit some self-similarity the deeper it went. I will focus mostly on the question of the potentially infinite depth of inquiry, where depth refers to gaining more knowledge that is not merely about the knowledge that one already has.

I will argue that the answer to the question: "could inquiry could be infinite?" highlights the goal-dependent nature of inquiry and understanding generally and that if there is a Richardson Effect to finding more facts, then goal-dependent and more pragmatist frameworks for metaphysics and epistemology are better ones. Just as the real Coastline "Paradox" resolves when we agree on a measurement criterion, so the philosophical skepticism of how we could know anything or be acquainted with any reality truly if it is in some deep sense fractal can be sidestepped when we share goals in understanding the world.

Clarification​

Admittedly, the general philosophical question of this note is, so far, unclear.

What if the relationship of inquiry to reality is fractal, like the relationship of a measured length to a coastline?

Let's clarify it a bit. There are two ways to interpret this question.

• Metaphysical Fractality

  Reality IS such that infinitely more detailed descriptions of phenomena will always be true of it.

This would mean that, whether we can know it or not, there is no rock-bottom to inquiry. The more facts we would discover, whether we were to discover them or not, the more other facts there will be to discover. It is important to note that, in order for this thesis to be interesting at all, these additional facts would not merely be "facts about the facts we already have", that is trivially true. The more facts we get, the more facts about facts there are. Fractal 'roughness' is not merely recursion.

Perhaps an example will help this point. Suppose physicists discover $G$-ons (some particle that describes all the other higher-level phenomena we know about) and the behavior of all the other things in the universe now makes sense. But wait! If Metaphysical Fractality is true, then we will likely subsequently discover that $G$-ons are composed of $H$-ons and $I$-ons etc etc and the process of discovery only moves 'downward' infinitely.

• Epistemological Fractality

  Our knowledge of reality is (and will be) such that a more detailed account will always avail itself (eventually) whenever a new less detailed one does.

Epistemological Fractality would mean that there is something, perhaps something necessary, about the nature of our knowledge and its relation to the world that makes it never reach able to reach rock-bottom, but always peels back another layer revealing new knowledge infinitely. Again, to be clear, it is trivially true the more knowledge we get, the more knowledge about that knowledge there is. That is not what is meant by Epistemological Fractality.

With either Epistemological Fractality or Metaphysical Fractality being true, a "coastline problem" emerges for our knowledge of the world. If Metaphysical Fractality is true, no matter what the nature of our inquiry is, there will never be an absolute fact that is not an infinite composite of deeper facts. If Epistemological Fractality is true, something about knowledge, but maybe not reality, yields the same effect.

Setting our metaphysical and epistemological baggage down for a minute, these two theories will be identical in most if not all of their predictions. Also, Depending on one's account of truth, these two theories might sound identical altogether. To avoid confusion and stick to the point here I will therefore treat them as the same.

I will cut a lot of philosophical corners here and revise our question to this:

Is either reality itself, or any possible knowledge we could have about it, fractal in nature? Is inquiry of infinite depth?

Perhaps to answer in the affirmative is just to adopt a certain disposition towards inquiry.

How Can We Answer?​

How might we answer the above question? Perhaps empirically? We can rephrase our question above as an empirical hypothesis. But is it actually testable? Its infinite nature muddles the meaning of its testability. Alternatively, maybe a rule that we firmly believe in guides us the conclusion that reality is fractal?

Empirically?​

Suppose, to continue with our mock-physics example, that we continue on to discover $Z$-ons, $A_2$-ons, $B_2$-ons, and eventually to $Z_2$-ons... $A...Z_{1001}$-ons.

The evidence always confers the same probability, at some observation $n$, on "infinite observations" as it does on "$n$ observations". So is it impossible to empirically decide? In the case of adding more observations, yes. However, in the case of observations completely ceasing it seems not. We could imagine a case where we discovered $Z_{1001}$-ons and that just tied everything up. That's it. Understanding is complete at the discovery of the $Z_{1001}$-on. Surely some will find this view absurd, but it is certainly possible unless we take a rather hardline commitment to Epistemological Fractality (or Metaphysical Fractality where we are ignorant of reality for some compelling reason).

If we admit that such a hard stop is possible and if we never observe such a hard stop, which we have not yet, then we have increasing evidence for reality being fractal with each layer of reality we peel back (but we do not have more evidence for it being fractal than for it only going as far as our present depth). This may or may not be significantly dependent on what prior probability we assign to reality being fractal in this way.

A Rule?​

The Fibonacci sequence is infinite. How do I know that? I know it because the Fibonacci numbers are the sequence of numbers

$\{F_n\}_{n=1}^\infty$

where

$F_n = F_{n-1} + F_{n-2}$

with $F_1 = F_2 = 1$, and conventionally defining $F_0 = 0$.

I know the rule to get the next number. Take the last two numbers, add them together and I get the next.

Given $0, 1, 1, 2$, I add $1+2$ and get $3$. It seems that I know that this can never end because I know a rule that, by virtue of my following it, necessarily gives me a new Fibonacci number.

Do we know such a rule for inquiries about reality generally: that they will always give me more facts or more questions left open? I do not think so (again, not in the sense of more 'facts about the facts', for that is trivially true). It seems necessarily true that the Fibonacci sequence will never terminate if I sat down and cranked out numbers for an infinite amount of time. It does not, in any salient way, seem necessarily true that one discovery unearths at least one more. However, if reality's fractality is not necessarily true or false, it follows as a simple truth of modal logic that it is possibly true.

An Answer​

Whether some rule would emerge that would conclusively show us that reality is or is not fractal or whether some hard-stop/rock-bottom would be observed that would prove that it is not, at present it seems that we have to accept that it is possible that reality is fractal in the sense suggested above.

The cash-value of believing that reality is possibly fractal with respect to inquiry, is a stance of preparedness for endless complexity and a disregard for the importance of ultimate ontological questions. For, if it is true that reality is possible fractal, then what there is, in reality, has no determinate answer unless we agree on a criterion, as in the coastline problem, for what we care about.

I think this highlights an already common-sense view. Who cares what the 'ultimate truth' of the coastline's length is if we are just trying to sail a boat around the coast of England in some finite amount of time? Who cares what the 'ultimate constituents of reality' are if we are just trying to survive, do good, launch a rocket, cure diseases, do the laundry, help future humans survive and flourish and so on. Only within these inquiries would it be worthwhile and possible to have an agreed on criterion of measurement (supposing reality is of this infinite fractal nature). Once we have such a criterion of measurement we no longer face indeterminacy about the answers.

This subject has in no way been treated with exhaustive clarity here and much more could be said about it. For the time being, I find it a fascinating lens for contemplating our relation to a world that is possibly intractably complex as creatures of finite attentive and computational power.

A scientist who ceases for a moment to try to solve his questions in order to inquire instead why he poses them or whether they are the right questions to pose ceases for the time to be a scientist and becomes a philosopher.

-- Gilbert Ryle, Philosophical Arguments

Intro​

I have too frequently heard skepticism expressed toward the usefulness (or worse: the epistemic viability) of armchair theorizing. The term "Armchair" is usually meant in pejorative sense to indicate that no real work could be done that way. I choose to just lean in to the term. Whether or not we take armchair theorizing to include mathematics, computer science, and logic this skepticism is unwarranted. There are a few subclasses of armchair theorizing that are usually in the crosshairs of those eager to criticize it. These typically include ethics, cosmology, analytic philosophy, theoretical physics, and much more. Given the amount of silly theorizing that goes on, the existence of criticism is unsurprising. However, I still see most of this criticism fall flat even when the analysis itself is not valid or useful.

Here I will argue that if we are going to accept any type of pure conceptual analysis as necessarily "Garbage in, Garbage out", which we should, then we are then committed to accepting it as necessarily "Gold in, Gold out". If we are committed to "Gold in, Gold out", then it follows that armchair knowledge can be generated and that should not be surprising.

Additionally, I will argue that the armchair toolkit consists of many useful tools that are not exhaustively described by 'listing facts', but nevertheless are indispensable in the furtherance of knowledge.

Naive Pure Empiricism​

Can we really generate knowledge from the armchair? How is that possible? I have myself been struck with a mysterious feeling around this question. If knowledge is about the world in some sense, how could I just sit here and come up with some? This may be an intuition only shared by those whom William James referred to as "hard-nosed empiricists" and they are mostly the target of the arguments here.

Philosopher David Chapman holds such a "hard-nosed" view with the only field allowed to generate armchair knowledge being mathematics:

If it were only this tweet where I had heard this sentiment expressed, I would likely just ignore it and move on. Indeed I would like to believe this position to be a straw-man I have invented, but sadly I have met many individuals who share this view, some deeply and some only on a superficial intuitive level.

I would like to interpret this charitably as "Don't speculate or try to reason abstractly too much about something that is best left to the domain of empirical research.", or maybe "We need SOME empirical content somewhere along the line to generate knowledge." I mostly agree with those and the second is something even most die-hard rationalists might accept. Chapman's words here invite a much stronger interpretation, even if maybe they are hyperbole. They espouse what I'll call Pure Naive Empiricism.

Let's slightly reformulate these claims while sticking to their cash-value as the formulation of Pure Naive Empiricism:

This claim is obviously false unless we adopt a rather extreme interpretation of what "empirical experiments" are. Pure Naive Empiricism appears to be a popular position among those not fond of abstraction that impinges on reality too closely. It would be a simple world if math and observations were all we needed for furthering knowledge.

Why is Pure Naive Empiricism entitled to stop at mathematics? (even if it is "mathematics plus some other stuff") If mathematics is an "acceptable" epistemic pursuit then why is formal reasoning about cosmology, ethics, metaphysics, or mind not? I suspect the Pure Naive Empiricist does not have a satisfactory answer to this question. We don't need to go poke anything to find out why either.

I will argue that there is no viable place to draw the line between "acceptable" and "not acceptable" analysis and so the distinction is bogus. Either all conceptual analysis of any kind (including mathematics) is capable of generating knowledge, if the premises are true and the rules are followed, or none of it is.

'Garbage In, Garbage Out' Implies 'Gold In, Gold Out'​

In learning elementary symbolic logic and my first programming languages I was taught a simple maxim of any deduction: "Garbage in, Garbage out." I believe this should uncontroversially apply to any formal language and indeed to everyday human languages in formulating and assessing arguments. Consider the following argument.

This is a valid argument but not a sound one. Nobody will ever care that Skrump is a Schmorg because it is a Blorg. We fed garbage in and we got garbage out.

What was not taught to me alongside this was "Gold in, Gold out". We usually don't have good reasons to care about this one because it is so obviously true. If we are writing a simple Python script that converts Celsius to Fahrenheit, we already know, trivially, that if it is 35^oC outside and my script says that converts to 95^oF, that this fact applies to the real temperature outside right now. We usually only need to be reminded of "Garbage in, Garbage out" when our analytical processes have generated an absurdity that we become convinced is true.

If the falsehood of at least one premise guarantees that a valid argument is not sound then all the premises truths guarantee that the argument is sound. We cannot rationally hold "Garbage in, Garbage out" without holding "Gold in, Gold out". If we have to hold both, then we cannot deny that the products of analysis are true. So, straightforwardly, if something is true and we have good reasons to believe it without other defeating reasons, we have knowledge.

If Armchair Knowledge Were Not Possible?​

Pure Naive Empiricism has extremely bizarre implications. For example, if all knowledge were generated solely by empirical experiments then we would have to know all of the conclusions entailed by our current beliefs, both the actual and conditional implications. We clearly don't know those. So either we claim that those somehow "are not knowledge" or we admit that Pure Naive Empiricism is a ridiculous view.

If armchair knowledge were not possible, how would we know what questions to ask to guide empirical inquiry? Should we be looking for consciousness in the brain? Do thoughts have a location? Can actual infinities exist? Could the universe be fundamentally random? Does it follow from space-time theory that space and time are not ontologically distinct? Is math real? Is everything we believe false because we only evolved to survive? Are these good questions at all? To find out if these questions are worth pursuing, we need armchair theorizing, even if it is speculative. We need to know that "this is the right/wrong question". The alternative is literally conducting an experiment to test every absurd hypothesis that we can come up with. Armchair theory, even speculative theory, can and does save us eons of unneeded experimentation.

Additionally, it is often overlooked by the Pure Naive Empiricist that not all knowledge-pursuing consists in the gathering of facts, deductively generated or discovered. We need to know the right questions and the right way to think about them to have success in any inquiry. Some ant colonies are complex systems whose behavior is best understood emergently. No listing of simple facts about these ants by itself, without the analytical armchair toolkit, would give us this insight.

What Armchair Theorizing Gets Wrong​

Some armchair theorizing is not worth the mental energy spent on it. If armchair knowledge can be knowledge at all, then it can be true, but what kind of armchair knowledge is useful? We should answer this question partially with reference to the two maxims above. I can say that I know that if "All Blorgs are Schmorgs and Skrump is a Blorg" then "Skrump is a Schmorg" but it is clearly of zero use whatsoever. The concepts we reason about, if we want to generate not only knowledge but knowledge that matters, must be clear and serve some end.

If we have some valid reasoning about minds, it is only as useful as the argument's concept of "minds" is related to the one(s) that we actually use. If we say minds are in rocks and atoms as well as in brains, then are we still talking about the same content anymore or have we made a move that makes our terms devoid of any of the predictive or explanatory power that made them useful? Perhaps in the future we will have some other theoretical reasons to shift the semantic ground away from the folk-concept of "minds".

Generally, we should be skeptical of armchair theorizing that overextends concepts beyond the scope of their reasonable usefulness. When that limit has been overreached is itself often a tricky philosophical question. Some philosophers believe that the Einsteinian notion of space-time should be scrapped because of analytic arguments about how time must be ontologically distinct from space. Though I cannot rule out these conclusions as false with a hand wave, we should be skeptical when armchair thinking has purportedly overturned a useful empirical framework.

What Can Armchair Theorizing Do?​

Every implication of our current beliefs, conceptual definitions, and strategies of inquiry is not laid bare before us just by having them. If that were the case, we would be supercomputers. That space needs to be mapped out and the edges of the map keep expanding. Useful armchair theory is not all pure deduction, sometimes it takes the form of reframing questions, guiding inquiry, and using the power of analogy to deepen understanding or see new possibilities. All of these modes and many more are indispensable to science and to good human lives.

Generally, useful armchair theory comes in the form of deductive arguments, clarifications of existing concepts, demonstrating the incompatibility of certain beliefs, the dispelling of illusory problems, the creation of new questions, meta-inquiry, and the discovery of unforeseen implications of currently known truths.

Conclusion​

I hope I have made it clear that outright denial of the possibility of non-experimental knowledge or 'armchair knowledge' is absurd. I have argued that it is irrational to reject the ability of analytical reasoning to generate knowledge and that it is wrong to limit the scope of the furtherance of knowledge to mere 'fact collection'. I think that the intuitions to the contrary are motivated by putting empirical inquiry on a pedestal while taking for granted the foundations that support it.

The analytic toolkit that can be accessed from the armchair cannot reach out and interface with the physical world, of course, but it simply does not need to in order to be useful, generate truth, and make lives better.